Sampling

library(tidyverse)
library(moderndive)

Quiz 1

• The balls are mixed before sampling to get a random sample
• Sampling variation explains why the 33 groups of friends did not all have the same numbers of balls that were red out of 50, and hence different proportions red.

Quiz 2

• Sampling 50 balls and 60% were red is not likely
• Sampling 50 balls and 40% were red is likely
• Sampling 50 balls and 5% were red if impossible
• Sampling 50 balls and 110% were red is impossible

Quiz 3

• Population is a collection of individuals or observations that you are interested in
• Population parameter is a numerical summary quantity about the population that is unknown, but you want to know
• Census is when you count all individuals or observations in the population in order to compute the population parameter’s value exactly
• Sampling is the act of collecting a sample from the population when you don’t have the means to perform a census
• Point estimate is a summary statistic computed from a sample that estimates an unknown population parameter
• Representative sampling is one that roundly looks like the population
• Sample is generalizable if any result based on the sample can generalize to the population
• Sample is biased when certain individuals or observations in a population had a higher chance of being included in a sample than others
• Sample is unbiased when every observation in a population had an equal chance of being sampled
• sample is random when we sample randomly from the population in an unbiased fashion
• infer is to deduce or conclude information from evidence and reasoning in your sampling activities

Quiz 4

virtual_samples_26 <- bowl %>% 
  rep_sample_n(size = 26, reps = 1100)

virtual_prop_red_26 <- virtual_samples_26 %>%
  group_by(replicate) %>%
  summarize(red = sum(color == "red")) %>%
  mutate(prop_red = red/26)

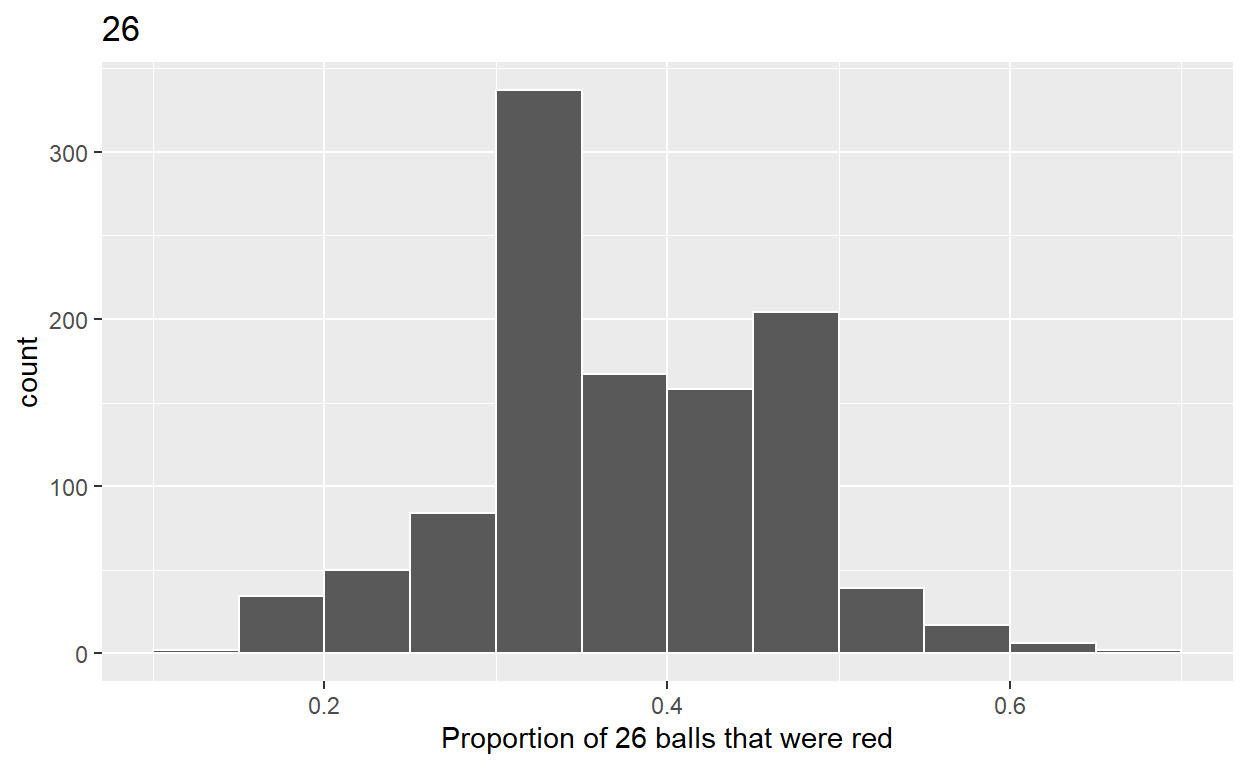
ggplot(virtual_prop_red_26, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 26 balls that were red", title = "26")

virtual_samples_57 <- bowl %>% 
  rep_sample_n(size = 57, reps = 1100)

virtual_prop_red_57 <- virtual_samples_57 %>%
  group_by(replicate) %>%
  summarize(red = sum(color == "red")) %>%
  mutate(prop_red = red/57)

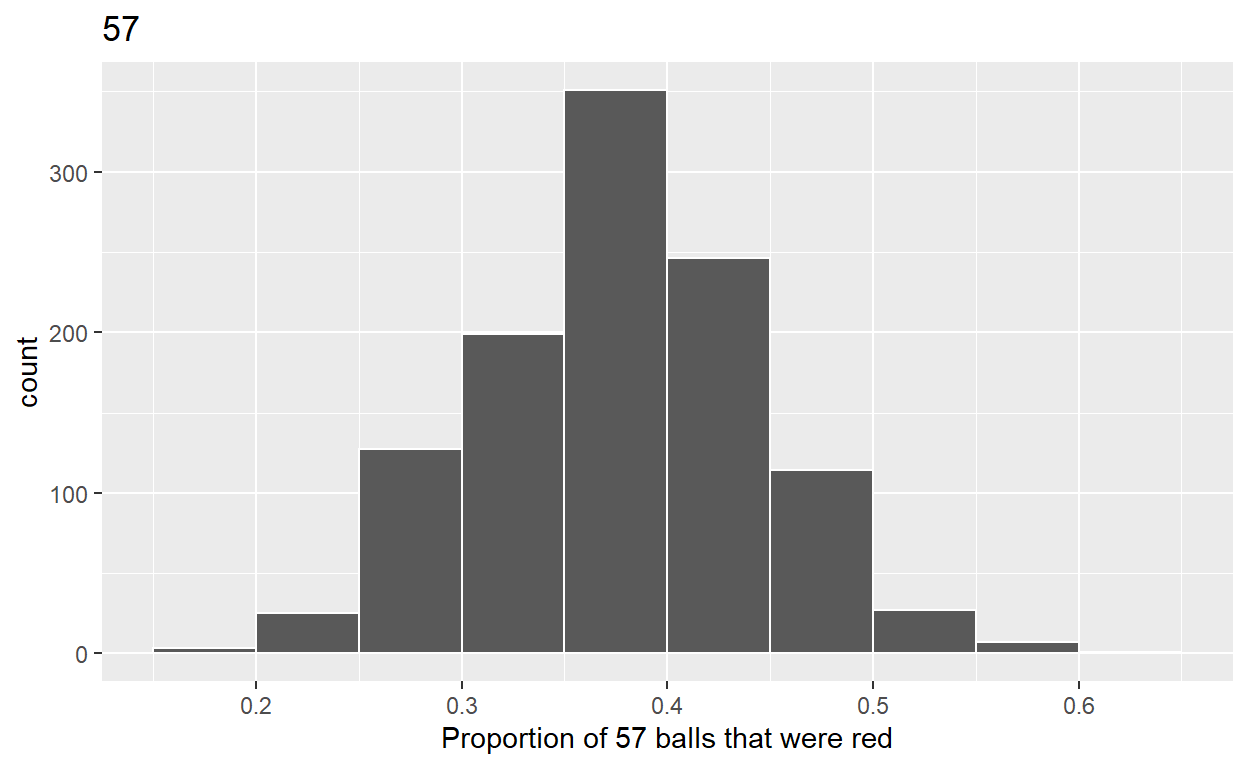
ggplot(virtual_prop_red_57, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 57 balls that were red", title = "57")

virtual_samples_110 <- bowl %>% 
  rep_sample_n(size = 110, reps = 1100)

virtual_prop_red_110 <- virtual_samples_110 %>%
  group_by(replicate) %>%
  summarize(red = sum(color == "red")) %>%
  mutate(prop_red = red/110)

ggplot(virtual_prop_red_110, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  labs(x = "Proportion of 110 balls that were red", title = "26")

calculate Standard deviation

virtual_prop_red_26 %>% summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0909

virtual_prop_red_57 %>% summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0651

virtual_prop_red_110 %>% summarize(sd = sd(prop_red))

# A tibble: 1 x 1
      sd
   <dbl>
1 0.0443

• The distribution with sample size, n = 110, has the smallest standard deviation (spread) around the estimated proportion of red balls